人教四年级数学下册总复习

第一单元 四则运算

1、加、减的意义和各部分间的关系

（1）把两个数合并成一个数的运算，叫做加法。

（2）相加的两个数叫做加数。加得的数叫做和。

（3）已知两个数的积与其中的一个加数，求另一个加数的运算，叫做减法。

（4）在减法中，已知的和叫做被就减数……。减法是加法的逆运算。

（5）加法各部分间的关系：

和=加数＋加数

加数=和－另一个加数

（6）减法各部分间的关系：

差=被减数－减数

减数=被减数－差

被减数=减数＋差

2、乘、除法的意义和各部分间的关系

（1）求几个相同加数的和和的简便运算，叫做乘法。

（2）相乘的两个数叫做因数。乘得的数叫做积。

（3）已知两个因数的积与其中一个因数，求另一个因数的运算，叫做除法。

（4）在除法中，已知的积叫做被除数…… 。除法是乘法的逆运算。

（5）乘法各部分间的关系：

积=因数×因数

因数=积÷另一个因数

（6）除法各部分间的关系：

商=被除数÷除数

除数=被除数×商

被除数=商×除数

（7）有余数的除法，

被除数=商×除数+余数

3、加法、减法、乘法、除法统称为四则运算

4、四则混和运算的顺序

（1）在没有括号的算式里，如果只有加、减法，或者只有乘、除法，都要按（从左往右）的顺序计算；

（2）在没有括号的算式里，如果既有乘、除法，又有加、减法，要先算（乘、除法），后算（加、减法）；（先乘除,后加减）

（3）在有括号的算式里，要先算括号里面的，后算括号外面的。

5、有关0的计算

①一个数和0相加，结果还得原数：

a + 0 =a 0 + a = a

②一个数减去0，结果还得这个数：

a － 0 = a

③一个数减去它自己，结果得零：

a － a = 0

④一个数和0相乘，结果得0：

a × 0 = 0 ; 0 × a = 0

⑤0除以一个非0的数，结果得0：

0 ÷ a = 0

⑥ 0不能做除数：

a÷0 = （无意义）

6、租船问题。

解答租船问题的方法：先假设、再调整。

第二单元 观察物体二

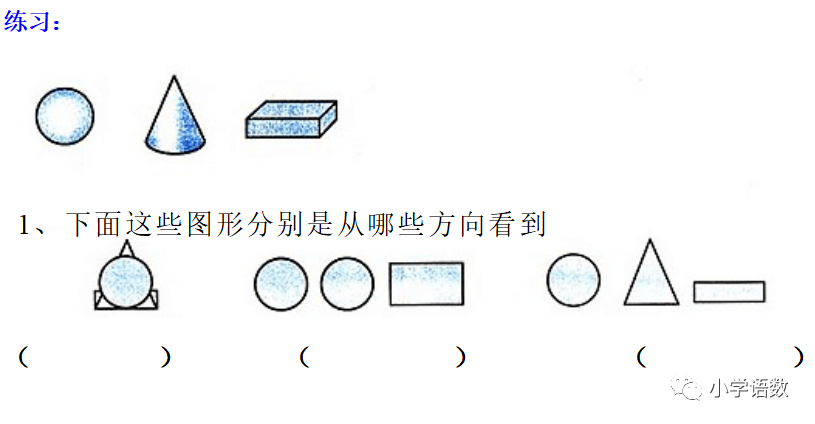
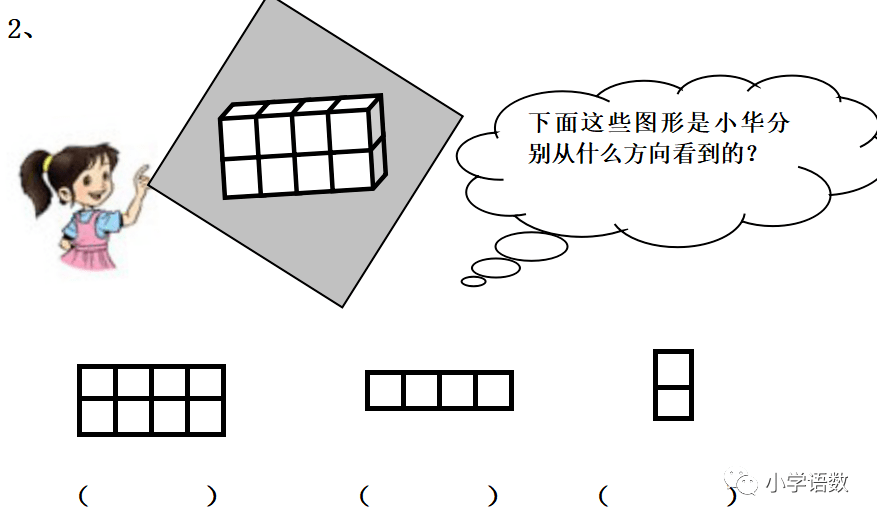
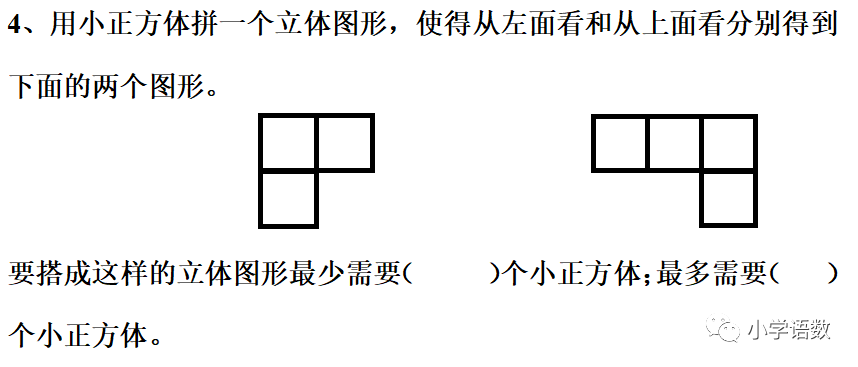
1、正确辨认从上面、前面、左面观察到物体的形状。

2、观察物体有诀窍，先数看到几个面，再看它的排列法，画图形时要注意，只分上下画数量。

3、从不同位置观察同一个物体，所看到的图形有可能一样，也有可能不一样。

4、从同一个位置观察不同的物体，所看到的图形有可能一样，也有可能不一样。

5、从不同的位置观察，才能更全面地认识一个物体。

【知识要点】

节日礼物（不同位置观察物体的范围不同）

1、随着观察位置的高低与远近变化，能判断出观察对象的画面所发生的相应变化。

2、根据观察到的画面，判断出观察者所在的位置。

红旗广场（不同位置观察物体的形状不同）

1、通过观察、比较一些照片，能够识别和判断拍摄地点与照片的对应关系。

2、通过观察连续拍摄到的一组照片，能够判断照片拍摄的前后顺序。

第三单元 运算定律

一、加法运算定律：

1、加法交换律：两个数相加，交换加数的位置，和不变。

a＋b＝b＋a

2、加法结合律：三个数相加，可以先把前两个数相加，再加上第三个数；或者先把后两个数相加，再加上第一个数，和不变。

(a＋b) ＋c＝a＋(b＋c)

3、加法的这两个定律往往结合起来一起使用。

如：165＋93＋35＝93＋（165＋35）

4、连减的性质：一个数连续减去两个数，等于这个数减去那两个数的和。

a－b－c＝a－(b＋c)

二、乘法运算定律：

1、乘法交换律：两个数相乘，交换因数的位置，积不变。

a×b＝b×a

2、乘法结合律：三个数相乘，可以先把前两个数相乘，再乘以第三个数，也可以先把后两个数相乘，再乘以第一个数，积不变。

(a×b) ×c＝a×(b×c)

乘法的这两个定律往往结合起来一起使用。

如：125×78×8的简算。

3、乘法分配律：两个数的和与一个数相乘，可以先把这两个数分别与这两个数相乘，再把积相加。

(a＋b) ×c＝a×c＋b×c

4、连除的性质：一个数连续除以两个数，等于除以这两个数的积。

a÷b÷c＝a÷(b×c)

乘法分配律的应用：

三、简便计算

1．连加的简便计算：

①使用加法结合律

（把和是整十、整百、整千、的结合在一起）

②个位：1与9，2与8，3与7，4与6，5与5，结合。

③十位：0与9，1与8，2与7，3与6，4与5，结合。

2．连减的简便计算：

①连续减去几个数就等于减去这几个数的和。

如：106-26-74=106-（26+74）

②减去几个数的和就等于连续减去这几个数。

如：106-（26+74）=106-26-74

3．加减混合的简便计算：

第一个数的位置不变，其余的加数、减数可以交换位置（可以先加，也可以先减）

例如：

123+38-23=123-23+38

146-78+54=146+54-78

4．连乘的简便计算：

使用乘法结合律：把常见的数结合在一起

25与4；125与8 ；125与80 等

看见25就去找4，看见125就去找8；

5．连除的简便计算：

①连续除以几个数就等于除以这几个数的积。

②除以几个数的积就等于连续除以这几个数。

6.乘、除混合的简便计算：

第一个数的位置不变，其余的因数、除数可以交换位置。（可以先乘，也可以先除）

例如：27×13÷9=27÷9×13

四、连除的性质：一个数连续除以两个数，等于除以这两个数的积。a÷b÷c= a÷(b×c)

1、常见乘法计算：

25×4＝100 125×8＝1000

五、简便计算示例：

加法和减法——找好朋友

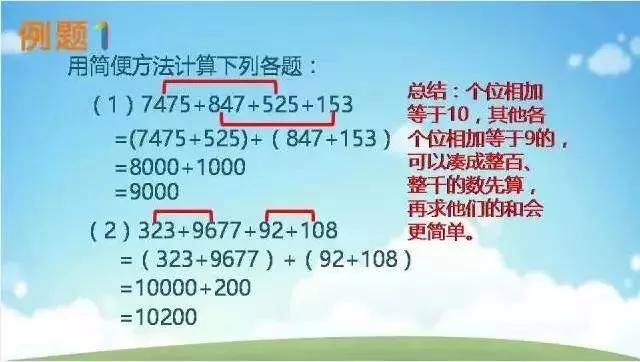
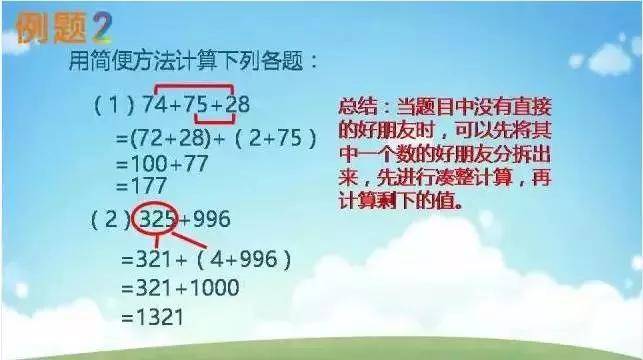
加法和减法——加括号

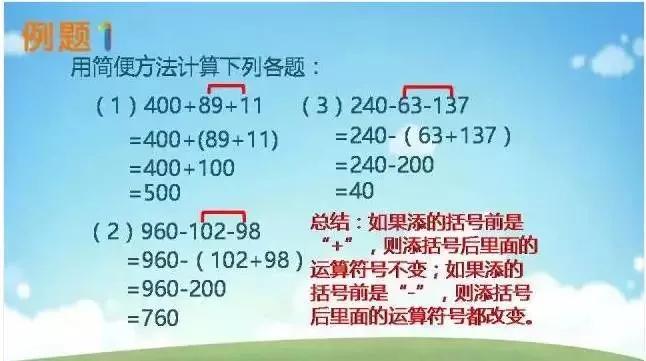
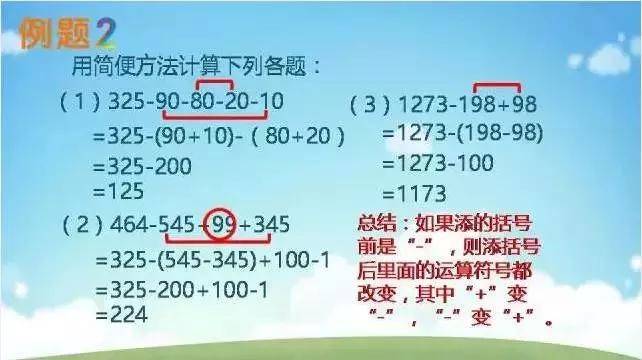
加法和减法——去括号

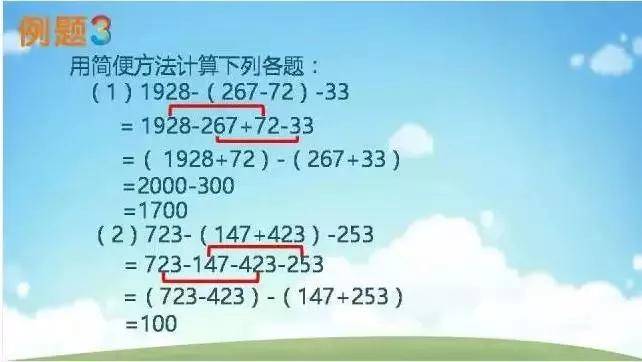
乘法和除法——找整与凑整

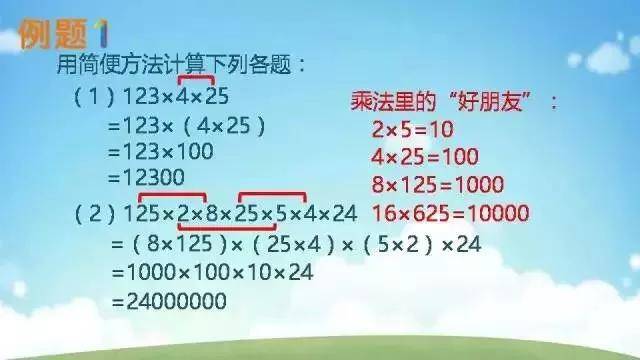
乘法和除法——乘法和加减法的混合运算

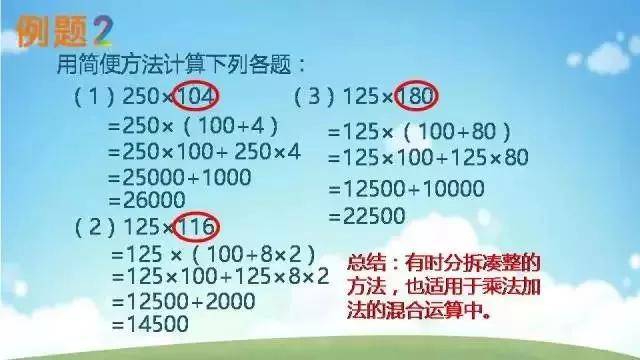
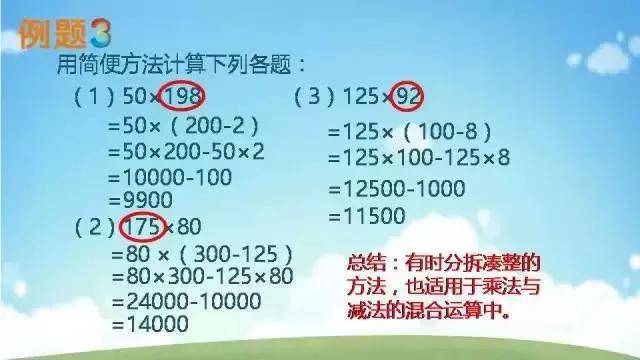
乘法和除法——乘除法混合运算

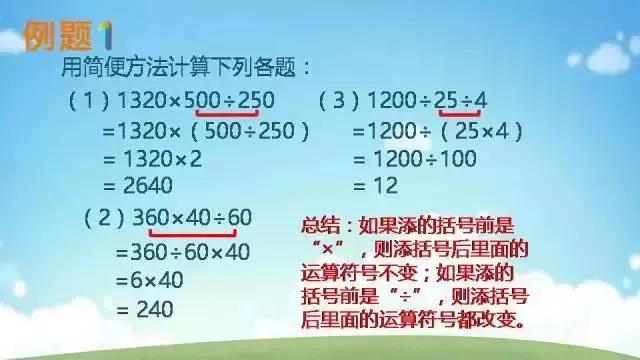
乘法和除法——除法和加减法的混合运算

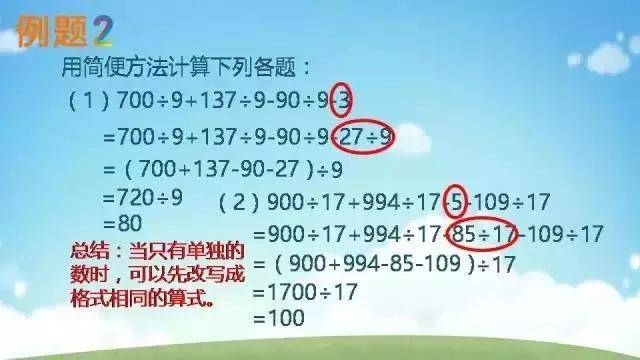
六、有关简算的拓展：

102×38－38×2

125×25×32

37×96+37×3+37

125×88

3.25＋1.98

10.32－1.98

易错的情况：

0.6+0.4-0.6+0.4

38×99+99

第四单元 小数的意义和性质

1、在进行测量和计算时，往往不能正好得到整数的结果，这时常用（小数）来表示。

分母是10、100、1000……的分数可以用（小数）来表示；

分母是10的分数可以写成（一位）小数，

分母是100的分数可以写成（两位）小数，

分母是1000的分数可以写成（三位）小数……

所以，一位小数表示（十分）之几，

两位小数表示（百分）之几，

三位小数表示（千分）之几……

如：

0.5表示（十分之五），

0.05表示（百分之五），

0.25表示（百分之二十五），

0.005表示（千分之五），

0.025表示千分之二十五）。

2、小数点前面的数叫小数的（整数）部分，小数点后面的数叫小数的（小数）部分，小数的数位是十分位、百分位、千分位……最高位是十分位。整数部分的最低位是个位。个位和十分位的进率是10。

3、小数的数位顺序表

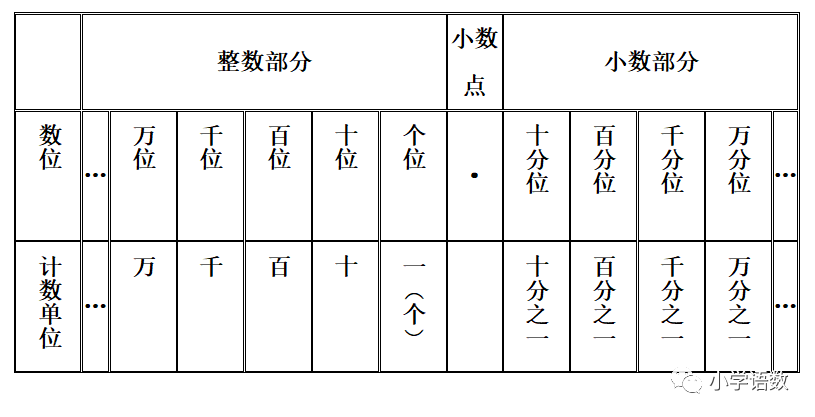
小数点后面第一位是（十）分位，十分位的计数单位是十分之一，又可以写作0.1；

小数点后面第二位是（百）分位，百分位的计数单位是百分之一，又可以写作0.01；

小数点后面第三位是（千）分位，千分位的计数单位是千分之一，又可以写作0.001……

如：（1）6．378的计数单位是0．001。（最低位的计数单位是整个数的计数单位）

（2）6．378中有6个一，3个十分之一（0．1），7个百分之一（0．01），

8个千分之一（0．001）。

（3）6．378中有（6378）个千分之一（0．001）。

（4）9．426中的4表示4个十分之一（0．1）[4在十分位]

（5）20.375，十分位上的3，表示3个（十分之一）；百分位上的7，表示7个（百分之一）；千分位上的5，表示5个（千分之一）。

4、小数每相邻两个计数单位间的进率都是10,（10个千分之一是1个百分之一，10个百分之一是1个十分之一，10个十分之一是整数1，或10个0.001是1个0.01 ,10个0.01是1个0.1, 10个0.1是整数1……

5、读小数时，整数部分按照整数的读法去读，小数点读作“点”，小数部分要依次读出每一个数字。读小数部分，小数部分要依次读出每个数字，而且有几个0就读几个0。

如：31.031读作：三十一点零三一

6、写小数时，整数部分按照整数的写法来写，小数点写在个位的右下角，小数部分要依次写出每一个数位上的数字。写小数部分，小数部分要依次写出每个数字，而且有几个0就写几个0。

如：一百二十点零零九八

写作：120.0098

7、在小数的末尾添上“0”或去掉“0”，小数的大小不变，这叫小数的性质。

注意：小数中间的“0”不能去掉，取近似数时有一些末尾的“0”不能去掉。作用可以化简小数等。

如：

0.2= 0.20 = 0.200 =0.2000 =……

1.05=1.050 =0.0500 =0.0500=……

1.080=1.08

10.0800=10.08

100.080000= 100.08

8、小数大小的比较：

先比较整数部分，整数部分大，那个小数就大；整数部分相同，就比较小数部分，十分位相同，就比较百分位，百分位也相同，就比较千分位……

9、小数点的移动：

（1）小数点向右：移动一位，相当于把原数乘10，小数就扩大到原数的10倍；移动两位，相当于把原数乘100，小数就扩大到原数的100倍；移动三位，相当于把原数乘1000，小数就扩大到原数的1000倍……

（2）小数点向左：移动一位，相当于把原数除以10，小数就缩小到原来的；移动两位，相当于把原数除以100，小数就缩小到原来的；移动三位，相当于把原数除以1000，小数就缩小到原来的……

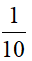
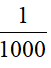
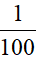
10、不同数量单位的数据之间的改写：

低级单位数÷进率=高级单位数

高级单位数×进率=低级单位数

当进率是10、100、1000……时，可以直接利用小数点的移动来换算。

（1）高级单位转化成低级单位==乘以进率，小数点向右移动。

（2）低级单位转化成高级单位==除以进率，小数点向左移动。

常用的单位：

质量：1吨＝1000千克； 1千克＝1000克

长度：千米＝1000米 1分米=10厘米

1厘米=10毫米 1分米=100毫米

1米＝10分米＝100厘米＝1000毫米

面积：1平方米＝ 100平方分米 1平方分米＝100平方厘米

1平方千米=100公顷 1公顷=10000平方米

人民币： 1元=10角

1角=10分 1元=100分

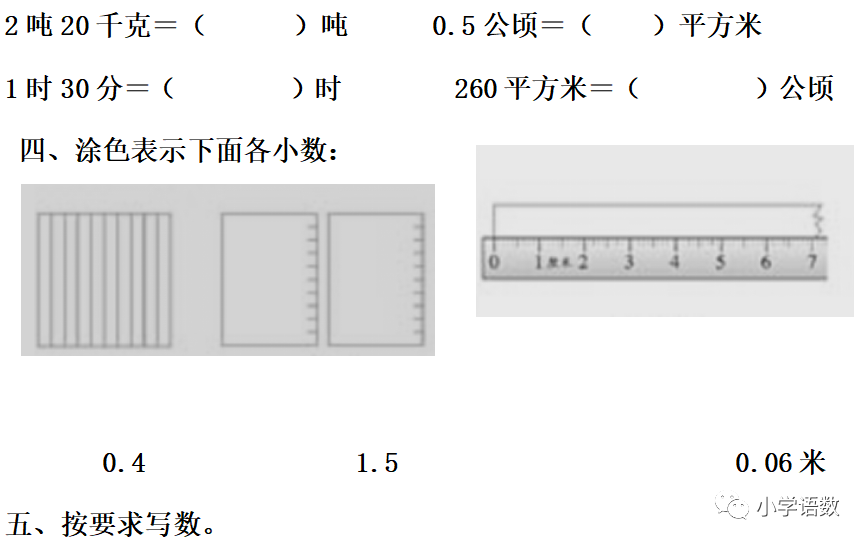
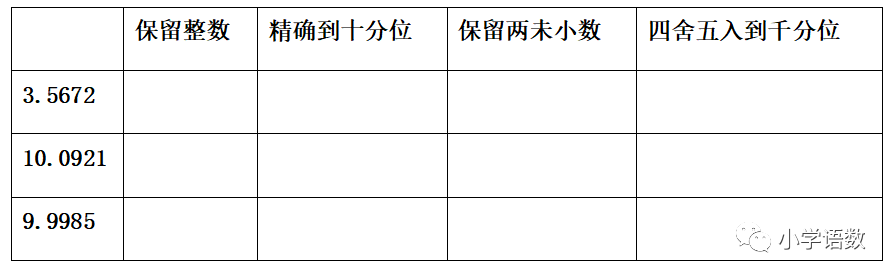
11、求近似数时：

（1）保留整数，表示精确到个位，就是要把小数部分省略，要看十分位，如果十分位的数字大于或等于5则向前一位进一。如果小于五则舍。

（2）保留一位小数，表示精确到十分位，就要把第一位小数以后的部分全部省略， 这时要看小数的第二位，如果第二位的数字比5小则全部舍。反之，要向前一位进一。

（3）保留两位小数，表示精确到百分位，就要把第二位小数以后的部分全部省略，这时要看小数的第三位，如果第三位的数字比5小则全部舍。反之，要向前一位进一。

（4）为了读写的方便，常常把不是整万或整亿的数改写成用“万”或“亿”作单位的数。改写成“万”作单位的数就是小数点向左移4位，即在万位的右边点上小数点，在数的后面加上“万”字。改写成“亿”作单位的数就是小数点往左移8位即在亿位的右边点上小数点，在数的后面加上“亿”字。注意：带上单位。然后再根据小数的性质把小数末尾的零去掉即可。

（5）（表示近似数时小数末尾的0不能去掉）

第五单元 三角形

1、三角形的定义：由三条线段围成的图形（每相邻两条线段的端点相连或重合），叫三角形。

2、从三角形的一个顶点到它的对边做一条垂线，顶点和垂足间的线段叫做三角形的高，这条对边叫做三角形的底。三角形只有3条高。重点：三角形高的画法。

3、三角形的特性：物理特性：稳定性。

如：自行车的三角架，电线杆上的三角架。

4、边的特性：任意两边之和大于第三边。

5、为了表达方便，用字母A、B、C分别表示三角形的三个顶点，三角形可表示成三角形ABC。

6、三角形的分类：

按照角大小来分：锐角三角形，直角三角形，钝角三角形。

按照边长短来分：三边不等的△，等腰△（等边三角形或正三角形是特殊的等腰△）。

等边△的三边相等，每个角是60度。（顶角、底角、腰、底的概念）

7、三个角都是锐角的三角形叫做锐角三角形。

8、有一个角是直角的三角形叫做直角三角形。

9、有一个角是钝角的三角形叫做钝角三角形。

10、每个三角形都至少有两个锐角；每个三角形都至多有1个直角；每个三角形都至多有1个钝角。

11、两条边相等的三角形叫做等腰三角形。

12、三条边都相等的三角形叫等边三角形，也叫正三角形。

13、等边三角形是特殊的等腰三角形

14、三角形的内角和等于180度。四边形的内角和是360°有关度数的计算以及格式。

15、图形的拼组：两个完全一样的三角形一定能拼成一个平行四边形。

16、用2个相同的三角形可以拼成一个平行四边形。

17、用2个相同的直角三角形可以拼成一个平行四边形、一个长方形、一个大三角形。

18、用2个相同的等腰的直角的三角形可以拼成一个平行四边形、一个正方形。一个大的等腰的直角的三角形。

19、密铺：可以进行密铺的图形有长方形、正方形、三角形以及正六边形等。

第六单元 小数的加减法

1、笔算小数加、减法的方法：

（1）小数点对齐，也就是相同数位对齐；

（2）从末位算起，算加法时，哪一位数相加满十都要向前一位进1；算减法时，哪一位不够减就要从前一位退1。

（3）得数末尾有 0，一般要把0去掉。

（4）不要忘记了小数点。

2、小数加减混合运算的顺序与整数加减混合运算的顺序相同：

（1）没有括号，按从左往右的顺序依次计算；

（2）有小括号，要先算小括号里面的。

3、整数的运算定律在小数运算中同样适用。在小数四则运算中，恰当地运用加法交换律、结合律及连减的运算性质会使计算更简便。

4. 得数是小数时，（末尾）的0一般要去掉。

5. 一个整数与一个小数相加减时：

① 先在整数的右边点上小数点；

② 再添上与另一个小数部分同样多个数的0；

③ 然后再按照小数加减法的计算方法计算。

6. 得数是小数时，（末尾）的0一般要去掉。

7、验算：

加法验算：

①交换加数的位置再加一遍，看结果与原来是否相同；

②用减法，把和减去一个加数，看差是否与另一个加数相同。

减法验算：

① 用加法，把减数与差相加，看结果是否等于被减数；

② 用减法，把被减数减去差，看是否等于减数。

应用整数运算定律进行小数的简便计算：

整数运算定律在小数运算中同样适用。在小数四则运算中，恰当地运用加法（交换律）、（结合律）及减法的运算性质会使计算更简便。

第七单元 图形的运动二

1、轴对称图形。

如果一个图形沿着一条直线对折，两侧的部分能够完全重合，这个图形就是轴对称图形，这条直线叫做对称轴。

（1）轴对称图形可能有一条对称轴，也可能有多条对称轴。

（2）图形重合时，互相重合的点叫做对应点。互相重合的线段叫做对应线段。

（3）称轴是一条直线，所以在画对称轴时，要画到图形外面，且要用虚线。

2、轴对称图形的性质和特征。

（1）对应点到对称轴的距离是相等的。连接对应点的连接线是互相垂直的。

（2）沿对称轴对折，对应点、对应线段都重合。

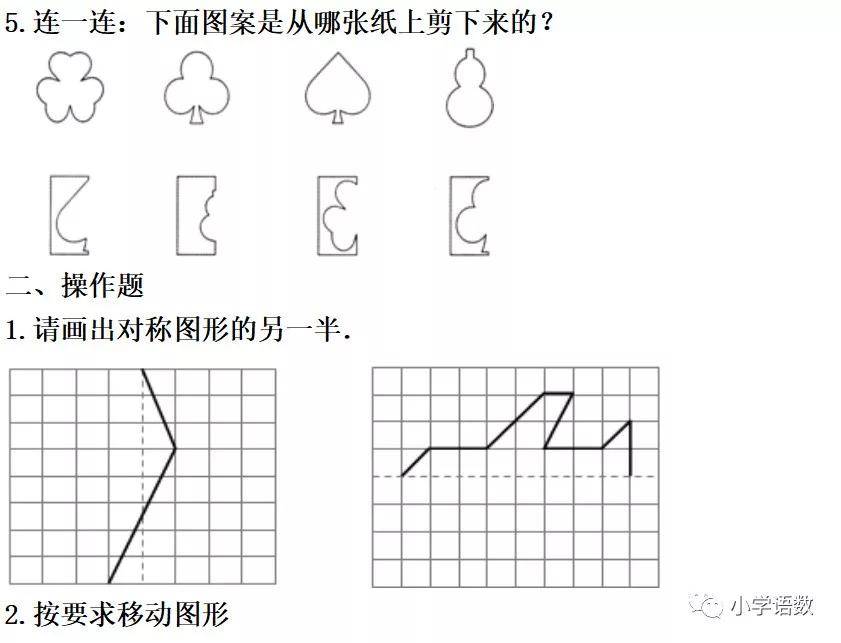
3、轴对称图形的画法。

（1）找关键点：找出图形的关键点，分别用字母表示。

（2）数格：数出这些点到对称轴有几格。

（3）描对称点：在对称轴的另一侧找出对应点，每组对应点到对称轴的距离相等地。

(4)连线：按顺序连接原图形关键点的对称点，就画出了所给图形的轴对称图形。

4、正方形的对角线所在的直线是它的对称轴。轴对称图形可以有一条或几条对称轴。

5、长方形、正方形、等腰梯形、等腰三角形、等边三角形、线段、菱形都是轴对称图形。

长方形有2条对称轴，

正方形有4条对称轴，

等腰梯形有1条对称轴，

等腰三角形有一条对称轴，

等边三角形有3条对称轴，

线段有1条对称轴，

菱形有2条对称轴，

圆有无数条对称轴，

半圆有一条，

圆环有无数条，

半圆环有一条。

6、平行四边形不是轴对称图形，没有对称轴。（长方形和正方形除外）

7、梯形不一定是轴对称图形。只有等腰梯形是轴对称图形。

8、古今中外，许多著名的建筑就是对称的。比如：中国的赵州桥，印度泰姬陵，英国塔桥，法国埃菲尔铁塔。

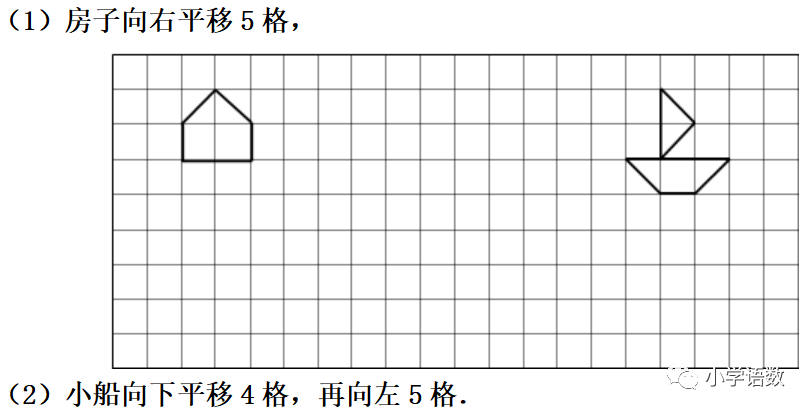
9、平移先找图形点，平移完点连起来，注意数点数要数十字。

10、平移不改变图形的大小、形状，只改变图形的位置。

11、利用平移，可以求出不规则图形的面积。

第八单元 平均数和条形统计图

平均数：

1.求平均数的方法：

(1)数据较少:移多补少法.

(2)常用方法：先合后分计算：

总数÷份数＝平均数

２.平均数能清楚地表示一组数据的整体水平。

条形统计图：

将两个单式条形统计图合并以后就得到一个复式条形统计图。

复式条形统计图要有图例。

复式条形统计图有横向和纵向两种。

复式条形 统计图 是用两个单位长度表示一个的数量，根据数量的多少画成长短不同的直条，

怎样画横向复式条形统计图

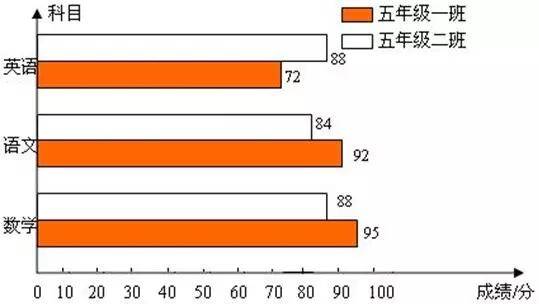
1.准备尺子，铅笔，橡皮等画图工具。

2.注意写单位，画中坐标和横坐标还有日期名字还有横坐标上的“0”。

3.假如位置有限，例如说0到10，到20，假如你写到200，位置绝对有限，你可以在0的上面画波浪线，然后写100（当然其他数也可以，但最标准的还是画闪电线）。

4.例如上图两者要有不同的颜色，假如没有色笔，第一个可以画斜线，第二个可以涂得严严实实。

5.在每个图的下方都要写标题。

复式条形统计图：

【特点】用直条的长短表示数量的多少。【优点】能清楚地看出数量的多少，便于比较两组数据的多少。

后把这些直条按一定的顺序排列起来。从复式条形统计图中很容易看出两者数量的多少。

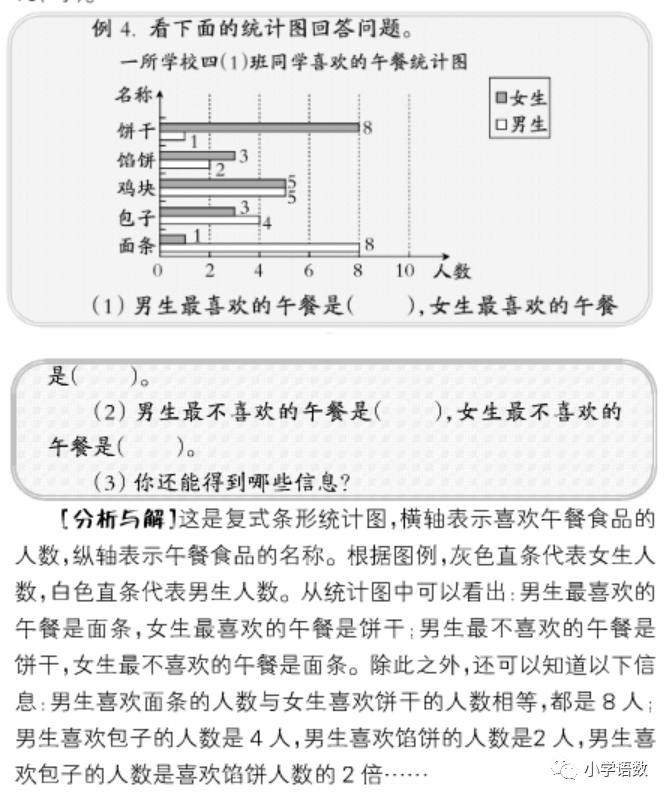
练习：

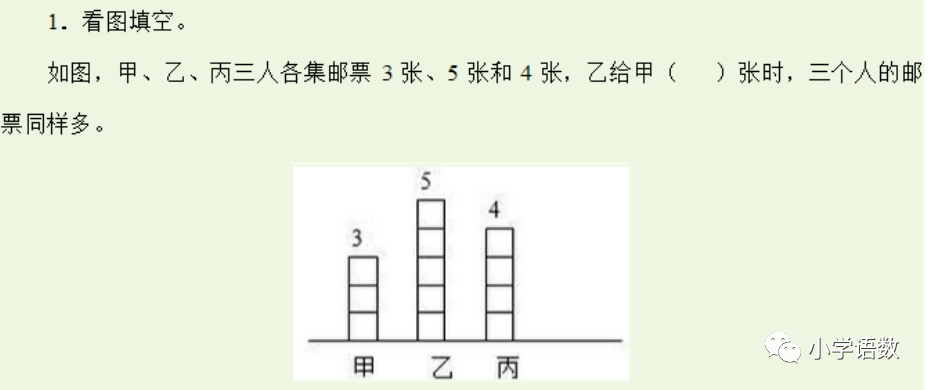
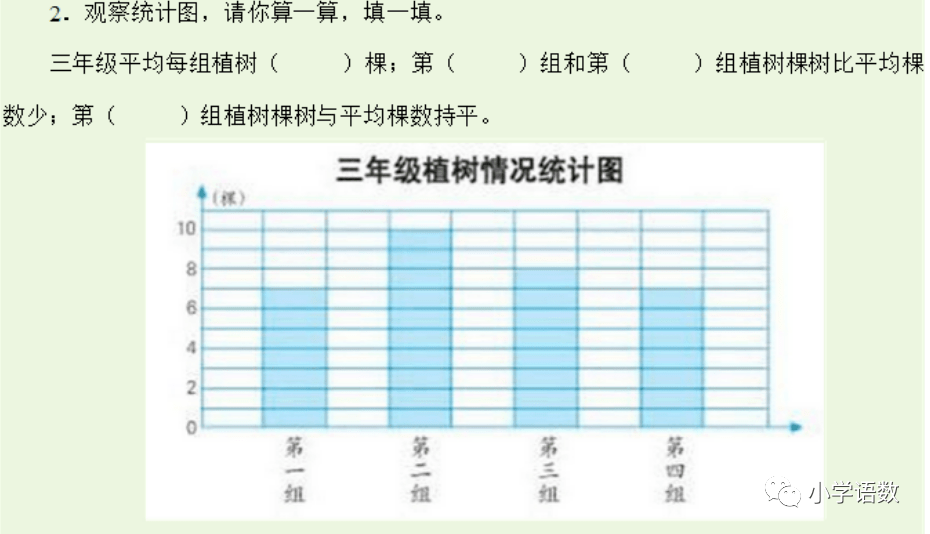
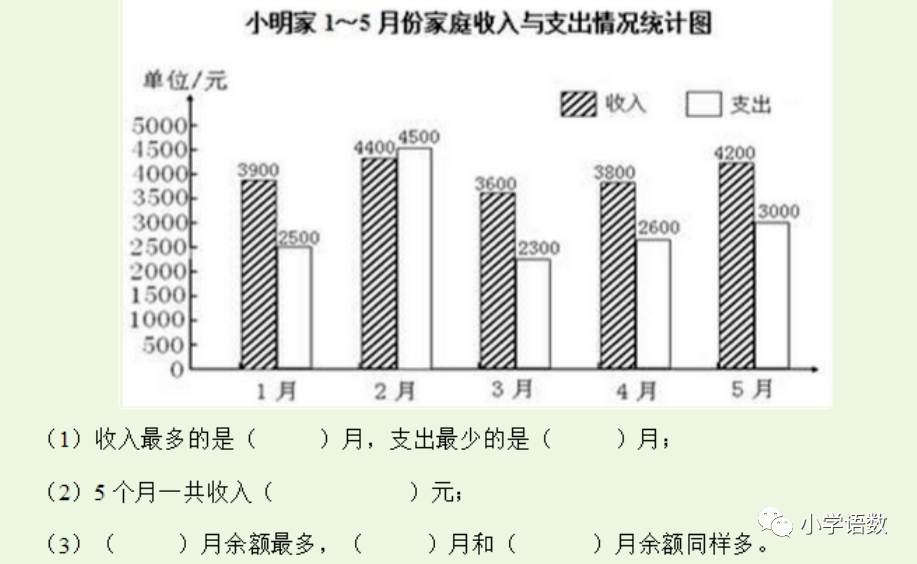
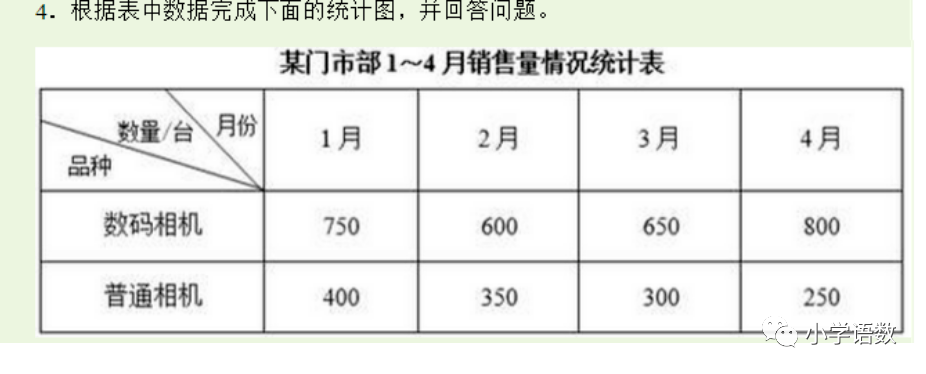
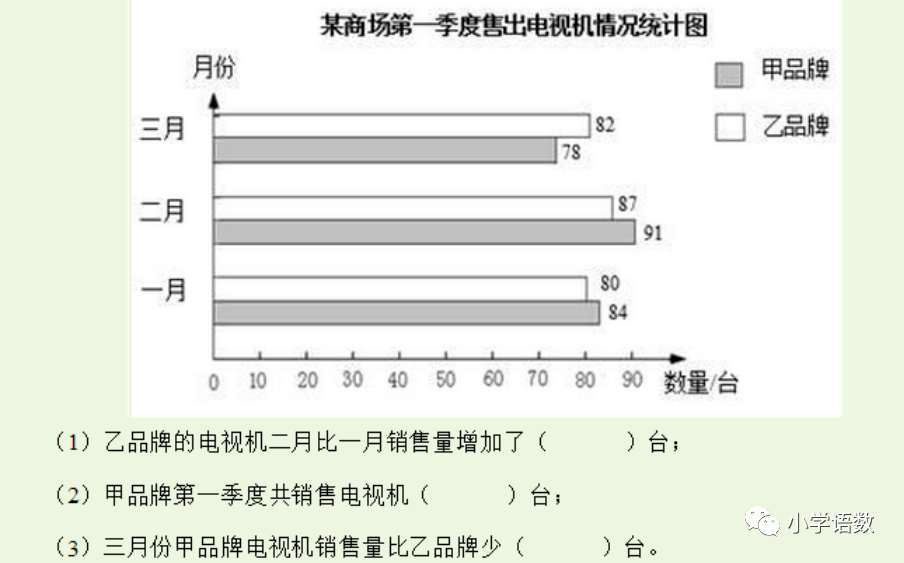
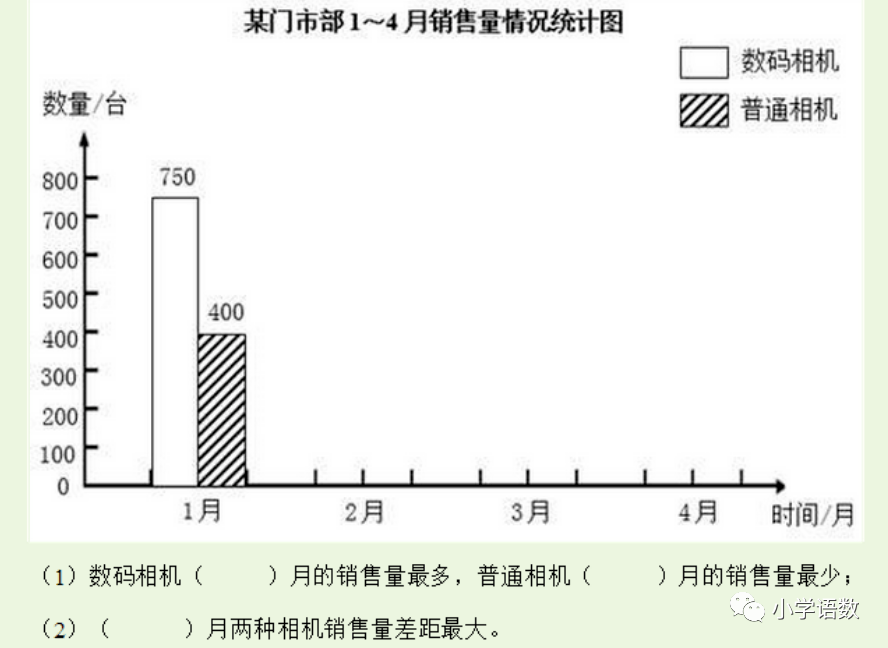
第九单元 数学广角-鸡兔同笼

“鸡兔同笼”问题

今有雉兔同笼， 笼子里有若干只鸡和兔。

上有三十五头， 从上面数，有35个头，

下有九十四足， 从下面数，有94只脚。

问雉兔各几何？ 鸡和兔各有几只？

猜一猜，鸡兔各有多少只？

鸡兔同笼，从上面数有8个头，从下面数，有26只脚，鸡和兔各有几只？

思路： 鸡有两只脚，兔有4只脚。

鸡兔可能有几只？可能只有一种动物吗，为什么？

不可能都是鸡，因为如果都是鸡就会有16只脚，而题目中是26只脚。也不可能都是兔，因为如果都是兔就会有32只脚。

解题方法：

1、列表法

观察表中的数据，你发现了什么规律？

鸡兔的总只数不变，每多一只鸡，就会少一只兔子，并会减少两只脚。

鸡兔的总只数不变，每多一只兔子，就会少一只鸡，并会增加两只脚。

2、假设法：

假设笼子里全都是鸡：

那么就有：2×8=16（只）

这样就多出：26-16=10（只）

一只兔子比一只鸡多2只脚，也就是有兔子数：10÷2=5（只）

鸡的只数：8-5=3（只）

答：笼子里有3只鸡，5只兔。

假设笼子里全都是兔：

那么就有：4×8=32（只）

这样就多出：32-16=6（只）

一只鸡比一只兔子少2只脚，也就是有鸡的只数：6÷2=3（只）

兔的只数：8-3=5（只）

答：笼子里有3只鸡，5只兔。

结论：

假设的方法

①假设笼子里全是鸡

兔的只数=(实际脚数-2×鸡兔的总只数)÷(4-2)

鸡的只数=鸡兔的总只数-兔的只数

②假设笼子里全是兔

鸡的只数= (4×鸡兔的总只数-实际脚数)÷ (4-2)

兔的只数=鸡兔的总只数-鸡的只数

所以鸡兔同笼问题又叫假设问题。

数学中一种重要的数学思想——假设思想。

你能试着用上面的方法解决前面的“鸡兔同笼”问题吗？

笼子里有若干只鸡和兔。从上 面数，有35个头，从下面数，有94只脚。鸡和兔各有几只？

假设笼子里全都是鸡：

那么就有：2×35=70（只）

这样就多出：94-70=24（只）

一只兔子比一只鸡多2只脚，也就是有兔子数：24÷2=12（只）

鸡的只数：35-12=23（只）

答：笼子里有23只鸡，12只兔。

假设笼子里全都是兔：

那么就有：4×35=140（只）

这样就多出：140-94=46（只）

一只鸡比一只兔子少2只脚，也就是有鸡的只数：46÷2=23（只）

兔的只数：35-23=12（只）

答：笼子里有23只鸡，12只兔。

做一做

1、有龟和鹤共40只，龟的腿和鹤的腿共有112条。龟、鹤各有几只？

2、新星小学“环保卫士”小分队12人参加植树活动。男生每人栽了3棵树，女生每人栽了2棵树，一共栽了32棵树。男、女生各有几人？

3、盒子里有大、小两种钢珠共30颗，共重266g。已知大钢珠每颗11g，小钢珠每颗7g。盒中大、小钢珠各有多少颗？

4、 鸡兔同笼，头共20个，足共62只，求鸡与兔各有多少只？

5、鸡兔同笼，头共35个，脚共94只，求鸡与兔各有多少个头？

6、在一个停车场上，停了汽车和摩托车一共32辆。其中汽车有 4个轮子，摩托车有3个轮子，这些车一共有108个轮子。求汽车和摩托车各有多少辆？